Some of the resources that I found helpful in learning Computer Science, Machine Learning, Maths, Physics, Quantum Computing etc. The resources I mention mainly consist of course material and lecture series, also all of them are open and freely accessible. The ones I found exceptional are highlited in yellow.
Mathematics
MIT 18.06
Lectures Course Page
For people you don't know this is the most watched MIT OCW course. The lectures are lucid and a delight to watch. Prof. Strang conveys the beauty of the subject delightfully. I guess his love for teaching is only surpassed by his love for Linear Algebra. He also has a book on the subject which is equally good.
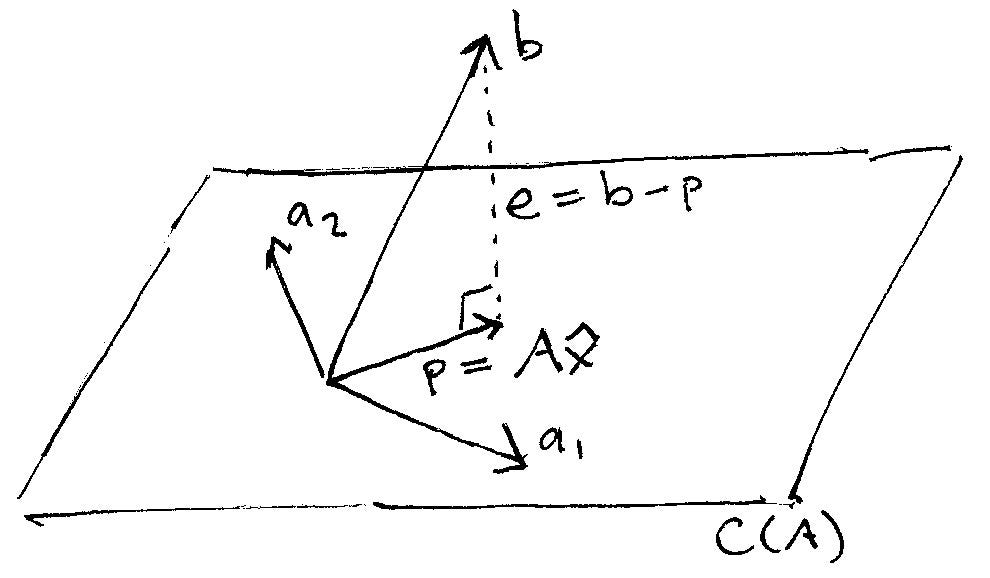
As far as the content is concerned, the course covers all the basics of Linear Algebra. It starts with the viewing systems of linear equation geometrically and the process of Gaussian elimination and how LU decomposition arises from it, then Prof. Strang moves onto teaching how to do matrix vector product in 4 different ways and interpretration of each of them.
Then he moves onto teaching about the four fundamental subspaces of a matrix and how they are related to each other.
Then he moves onto teaching about Orthogonality, Gram-Schmidt Process, Determinants, Eigenvalues and Eigenvectors, Diagonalization, Exponentiating a matrix, Positive Definite Matrices, Singular Value Decomposition, etc.
Linear Algebra is a very useful subject and this course is a probably the best way to learn it.
I would also recommend you watch 3blue1brown's Essence of Linear Algebra series on YouTube. It's also a great way to get an intuition about the subject.
MIT 18.02
Lectures Course Page
Honestly before I started this course I didn't hope to learn much since I had already learned Multivariable calculus in tids and bits from Khan Academy's video series. But I ought to say the course both exceeded my expectations and I actually quite a bit of stuff which I didn't know. Especially want to mention Prof. Dennis Auroux who gave us in my opinion probably one of the best MIT OCW courses. Coming to the course contents. The course starts with basics of vectors, which may be skipped. But thanks to section I finally learned the proof of why dot product (multiplying and adding a bunch of numbers) measure the angle between two vectors, proof of why cross product being equal to the area of the parallelogram and perpendicular to the initial vectors. He then covers basic matrix algebra, determinants and parametric equations. The section ends with Prof. Auroux proving Kepler's 2nd law analytically for any radial fields using only vectors, which was an interesting proof.
The next section is about differential multivariable calculus. He covers Partial derivatives, how df = fxdx + fydy arises from the tangent approximation to the plane, minimizing and maximizing multivariable functions and the proof of why determinant of Hermitian Matrix must be strictly positive. He then goes on to multivariable chain rule, gradients, lagrange multiplier, partial derivatives in case of non-independent variables (my favourite topic from this section).
The final section is Integral multivariable calculus. He starts with Double Integrals, then doing these in Polar coordinates, proving how Jacobian Matrices arise from change of variables. He then discusses Line Integrals, Path Independence and Gradient fields. He then discusses Green's theorem, proof of Green's theorem (most elegant proof in the course in my opinion) and Flux in 2D. Then he moves on to 3D Integrals, doing them in rectangular, spherical, cylindrical coordinates. He then discusses surface integrals in 3D and the divergence theorem and finally line integrals in 3D and the Stoke's theorem. Also not to mention the final 2 lectures reviewing the course content.
Anyone doing the course must do the Assignments and the Supplementary excercises, afterall Maths is not a passive subject. All in all, I learnt a lot from this course and I ought to say some of this by the end of course may feel like second nature.
MIT 18.03
Lectures Course Page
This course is taught by late Prof. Arthur Mattuck. For people who don't know, he is the person behind MIT's Undergraduate Maths curriculum and course structuring. Especially the calculus sequence 18.01, 18.02, 18.03.
Prof. Mattuck is a really humourous and witty lecturer. He is absolutely clear in his presentations and knows how to convey ideas lucidly.
Regarding the course contents - the course starts out with Direction Field, Numerical Methods for solving ODEs, First Order Linear ODEs and Autonomous DEs. Though I had done some Differential Equations before, but most of these introductory topics were new to me.
He then moves on to complex numbers, exponentiating DEs to complex Differential Equations, Second Order homogenous ODEs with constant coefficients.
Solving Inhomogenous Second-Order ODEs, Damped Oscillations and Resonance. By the end of this section, one will gain very solid understanding of solving second-order ODEs.
The second half of the course is focused on Fourier Series and solving DEs using Fourier Series, Laplace Transform (my favourite topic in the course), Impulse and Step Response. This portion was probably my favourite.
The last quarter of the course deals with Systems of Equations - Decoupling systems, Exponentiating Matrices, Sketching Solutions for System ODEs (another favourite of mine) and finally Linearing Non-linear Systems, Limit Cycles and Volterra Principle.
The course as a whole is excellent and a must do for any engineering stduent. Also I recommed doing the Problem Sets and the Supplementary Excercises given in the Reading. Maths is not a passive subject, therefore doing these excercises are a must to gain full understanding of the subject.
The only reason I am not highlighting this course in yellow is because of poor video quality of the lectures, MIT should upscale these videos using Neural networks. But still the teaching by Prof. Mattuck makes the course worth watching each minute of it.

Harvard - Stat 110
Lectures
I watched this course alongside my own Probability and Random Process (PRP) course in college. My course lecturer was fine, but I was somewhere missing the insights which Prof. Joe Blitstein provides in his lectures.
He has an unique way of proving things using what he calls 'story proofs', he proves using standard techniques as well but story proofs are more creative and fun.
His lectures are a good mix of application, theory and especially really interesting problems.
He has a book on this subject and I ought to say the problems at the end of each chapter are probably the most unique ones, saying this after TAing PRP the next year.
Joe does a great job of making the questions interesting, creative (most of the questions are not the same old Monty Hall), instructive and clear.
I highly recommend his lectures videos and book to anyone who wants to learn Probability, a very useful subject in general and especially in today's time because of rise of Data Science, Machine Learning.
MIT 6.042J
Lectures Course Page
This course is taught by two professors Prof. Tom Leighton and Prof. Marten van Dijk. I didn't see much part of Prof. Marten, since some of his content I already knew.
But I have watched all the lectures by Prof. Tom Leighton and I ought to say he is a delight to watch. No joking but each lecture of his is a performance in itself and If I were at MIT, I wouldn't mind giving a standing ovation at the end of each of his lecture.
To top it off, he is also the CEO of Akamai Technologies, which is a multi-billion dollar company.
Talking about the course content, the course is mainly about discrete mathematics for computer science and engineering.
Topics covered include formal logic notation, proof methods, induction, well-ordering, sets, relations, elementary graph theory, integer congruences, asymptotic notation and growth of functions, permutations and combinations, counting principles, state machines and invariants, recurrences, generating functions discrete probability.
Every Computer Science student should know this stuff and this course is a great way to learn it.
Computer Science
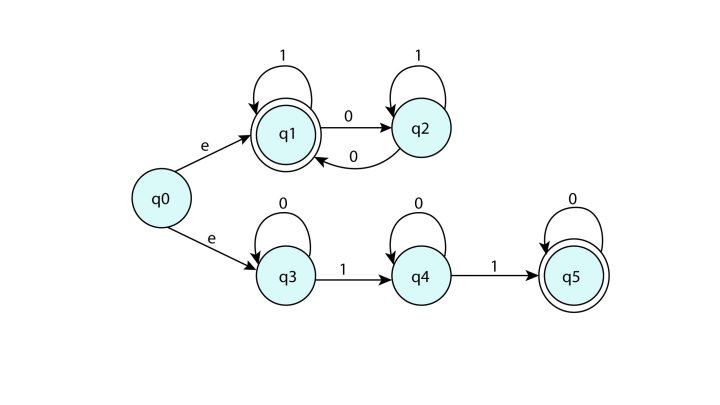
MIT 18.404J
Lectures Course Page
Prof. Sipser has a very famous book on this subject. The lectures are based on his book and are excellent.
The first half of the course is about Computability Theory. This half is focused on abstracting the mathematical model of a Computer.
It starts with the basics of Discrete Finite Automata and progressively builds up to Turing Machines.
Over the course, you will learn about various problems that are unsolvable by each computational problem including the famous Halting Problem.
The second part of the course is about Complexity Theory. It covers Time-Complexity, NP-completness, Cook-Levin Theorem, reducting problems to SAT, Space-Complexity, Savitch's Theorem, Hierarchy Theorem, L, Nl, coNL, Probabilistic Computation and Interactive Proofs.
Prof. Sipser really made me fall in love with Complexity Theory.
The lectures are really interesting and provide a lot of intuition and insights about the topic. I highly recommend solving the end of chapter problems from his book as well. They are really challenging and fun to think about!
Machine Learning
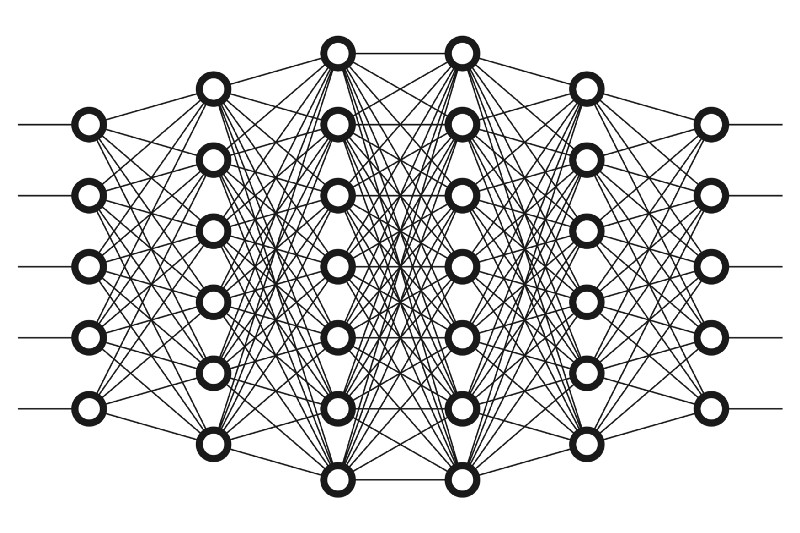
CMU 11-485/785
Lectures Course Page
I have personally watched all the lectures from this series and solved the assignments.
This course has honestly made me respect CMU a lot.
Before I watched these lectures, I had no idea about CMU having such amazing courses or CMU in general.
Prof. Biksha Raj really teaches the concepts in a very visual and lucid manner.
The topics covered go from Multi layered Perceptrons all the way up to CNNs, RNNs, Transformers, GANs, Diffusion Models, Boltzmann Machines, Autoencoders, VAEs, etc.
The first part of the Assignments consist of implementing a library from scratch similar to PyTorch just using Python and Numpy.
The second part of the Assignments are an open kaggle competition and you are allowed to use PyTorch for that.
The course is completely from scratch and does not assume any prior knowledge of ML and DL. The course covers all the topics in detail and even the breadth of topics is huge.
I honestly cannot recommend this course enough!